問1
次の各文章の[1]~[13]の中に入れるべき最も適切な字句等をそれぞれの解答群から選び、その記号を答えよ。(配点計50点)
(1)RC直列回路
図1に示すように、電圧\(\mathrm{\dot{V}}\)角周波数ωの交流電源に、静電容量Cのコンデンサと可変抵抗が接続され、電流\(\mathrm{\dot{I}}\)が流れている。このとき、可変抵抗の抵抗値Rを調整して、消費される電力を最大にする手順を考える。ここで、電圧\(\mathrm{\dot{V}}\)の大きさをV、電流\(\mathrm{\dot{I}}\)の大きさをIとする。
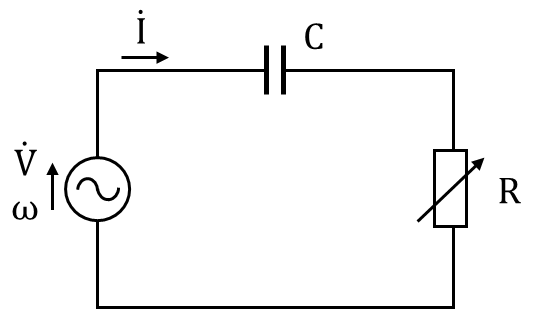
図1
1)可変抵抗で消費される電力
まず、図1においてコンデンサと可変抵抗の合成インピーダンスZの大きさは次式のように表される。
\[\mathrm{Z=\colorbox{cyan}{[ 1 ]} \tag{1}}\]
したがって、可変抵抗で消費される電力Pは、電流Iを求めて、次式のように表される。
\[\mathrm{P = I^{2}R = \frac{(\omega C)^{2} V^{2}}{\colorbox{cyan}{[ 2 ]}} \tag{2}}\]
(ア)\( \displaystyle \mathrm{\sqrt{R^{2}+(\omega C)^{2}}} \)
(イ)\( \displaystyle \mathrm{\sqrt{R^{2}+\frac{1}{(\omega C)^{2}}}} \)
(ウ)\( \displaystyle \mathrm{\sqrt{\frac{1}{R^{2}}+(\omega C)^{2}}} \)
(エ)\( \displaystyle \mathrm{1+(\omega CR)^{2}} \)
(オ)\( \displaystyle \mathrm{\frac{1}{R}+(\omega C)^{2}R} \)
(カ)\( \displaystyle \mathrm{\frac{1}{R^{2}}+(\omega C)^{2}} \)
[1](イ)\( \displaystyle \mathrm{\sqrt{R^{2}+\frac{1}{(\omega C)^{2}}}} \)
[2](オ)\( \displaystyle \mathrm{\frac{1}{R}+(\omega C)^{2}R} \)
2)最大電力
次に式(2)の最大値Pmaxを考える。
ⅰ)式(2)において、変数をRとし、式の分子(ωC)2V2をA、分母をB(R)と置くと、\(\displaystyle\mathrm{\frac{A}{B(R)}} \)が最大になるためには分母のB(R)が最小になればよい。この例では、B(R)の変化を考慮すると、B(R)が最小となるのはRが\(\displaystyle\mathrm{\frac{d}{dR}B(R)=0}\)を満たすときである。ここで、\(\displaystyle\mathrm{\frac{d}{dR}B(R)}\)は次式のように表される。
\[\mathrm{\frac{d}{dR}B(R)=\colorbox{cyan}{[ 3 ]} \tag{3}}\]
ⅱ)式(3)が零になる変数R(正の実数)を選ぶことにより、消費電力が最大となるときの抵抗値Rが求まる。これを式(2)に代入することにより、Pmaxは次式のように求められる。
\[\mathrm{P_{max}=\colorbox{cyan}{[ 4 ]} \tag{4}}\]
(ア)\( \displaystyle \mathrm{-\frac{2}{R^{3}}} \)
(イ)\( \displaystyle \mathrm{2(\omega C)^{2}R} \)
(ウ)\( \displaystyle \mathrm{-\frac{1}{R^{2}}+(\omega C)^{2}} \)
(エ)\( \displaystyle \mathrm{\frac{\omega C}{2}V^{2}} \)
(オ)\( \displaystyle \mathrm{\frac{(\omega C)^{2}}{2}V^{2}} \)
(カ)\( \displaystyle \mathrm{\frac{1}{2(\omega C)}V^{2}} \)
[1](ウ)\( \displaystyle \mathrm{-\frac{1}{R^{2}}+(\omega C)^{2}} \)
[2](エ)\( \displaystyle \mathrm{\frac{\omega C}{2}V^{2}} \)
解説
交流回路のインピーダンスおよび電力の計算方法について解説していきます。
インピーダンスの計算
静電容量CのコンデンサのインピーダンスをXCとすると、XCは次式で表される。
\[\mathrm{X_{C}=\frac{1}{\omega C}\tag{5}}\]
交流回路のインピーダンスはベクトル上で計算する必要がある。抵抗RとコンデンサのインピーダンスXCをベクトルで表すと図3となる。
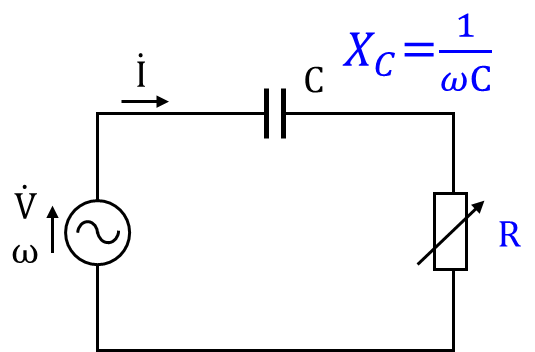
図2 RC回路のインピーダンス
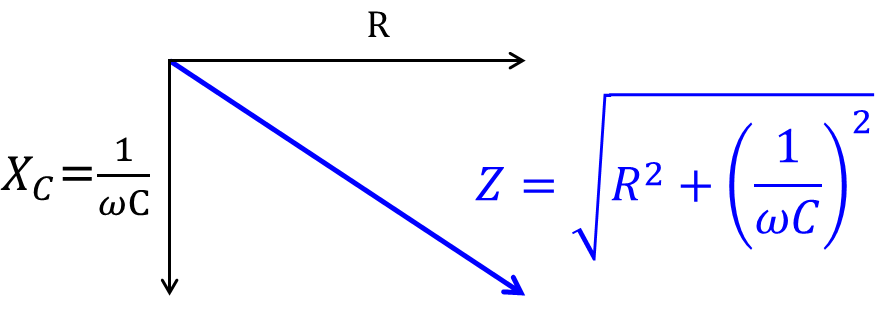
図3 RC回路のベクトル
回路全体のインピーダンスZは三平方の定理より、抵抗RとコンデンサのインピーダンスXCの二乗和の平方根となるので、次式となる。
\[\mathrm{Z=\sqrt{R^{2}+\frac{1}{(\omega C)^{2}}}\tag{6}}\]
電力の計算
図2のRC直列回路の電力は次式で表される。
\[\mathrm{P=I^{2}R=\left(\frac{V}{Z}\right)^{2}R\tag{7}}\]
式(7)に式(6)を代入すると、
\[\mathrm{P=\left(\frac{V}{\sqrt{R^{2}+\frac{1}{(\omega C)^{2}}}}\right)^{2}R\tag{8}}\]
\[\mathrm{P=\frac{(\omega C)^{2}V^{2}}{\frac{1}{R}+(\omega C)^{2}R} \tag{9}}\]
式の展開が多いので計算ミスに注意しましょう。
最大電力の条件
式(9)の電力が最大となる時は、分母が最小の時である。よって、最大電力の条件は次式で表される。
\[\mathrm{\frac{d}{dR}\left(\frac{1}{R}+(\omega C)^{2}R\right)=0}\]
\[\mathrm{\frac{d}{dR}\left(\frac{1}{R}+(\omega C)^{2}R\right)=-\frac{1}{R^{2}}+(\omega C)^{2}=0}\]
\[\mathrm{R=\frac{1}{\omega C}\tag{10}}\]
つまり、最大電力となるのは、可変抵抗Rとコンデンサのインピーダンスが等しい時である。これは、よく出題されるので覚えておきましょう。
最大電力の計算
式(10)を式(8)に代入すると、
\[\mathrm{P_{max}=\left(\frac{V}{\sqrt{\frac{1}{(\omega C)^{2}}+\frac{1}{(\omega C)^{2}}}}\right)^{2}\frac{1}{\omega C}}\]
\[\mathrm{P_{max}=\frac{\omega C}{2}V^{2}}\]









コメント